Behavior of coupled DEVS

DEVS is closed under coupling [Zeigper84] [ZPK00]. In other words, given a coupled DEVS model $N$ , its behavior is described as an atomic DEVS model $M$ . For a given coupled DEVS $N$ , once we have an equivalent atomic DEVS $M$ , behavior of $M$ can be referred to behavior of atomic DEVS which is based on Timed Event System.

Similar to behavior of atomic DEVS, behavior of the Coupled DEVS class is described depending on definition of the total state set and its handling as follows.

1 View1: Total States = States * Elapsed Times
2 View2: Total States = States * Lifespan * Elapsed Times
3 Time Passage
4 Remarks
5 See also
6 References

View1: Total States = States * Elapsed Times

Given a coupled DEVS model 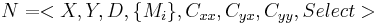$N = <X,Y,D,\{M_i\},C_{xx}, C_{yx}, C_{yy}, Select>$ , its behavior is described as an atomic DEVS model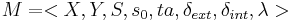 $M = <X,Y,S,s_0,ta, \delta_{ext}, \delta_{int}, \lambda>$

where

$X$ and $Y$ are the input event set and the output event set, respectively.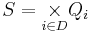
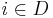$S=\underset{i \in D}\times Q_i$ is the partial state set where $Q_i=\{(s_i,t_{ei})| s_i \in S_i, t_{ei} \in (\mathbb{T} \cap [0, ta_i(s_i)])\}$ is the total state set of component $i \in D$ (Refer to View1 of Behavior of DEVS), where 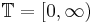$\mathbb{T}=[0,\infty)$ is the set of non-negative real numbers.
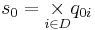$s_0=\underset{i \in D}\times q_{0i}$ is the initial state set where 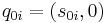$q_{0i}=(s_{0i},0)$ is the total initial state of component $i \in D$ .
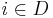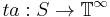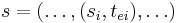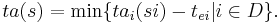
$ta:S \rightarrow \mathbb{T}^\infty$ is the time advance function, where $\mathbb{T}^\infty=[0,\infty]$ is the set of non-negative real numbers plus infinity.Given $s=(\ldots, (s_{i},t_{ei}),\ldots)$ , $ta(s)= \min\{ ta_i(si) - t_{ei}| i \in D\}.$

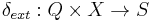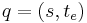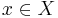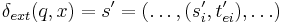
$\delta_{ext}:Q \times X \rightarrow S$ is the external state function. Given a total state $q=(s,t_e)$ where $s=(\ldots, (s_{i}, t_{ei}),\ldots), t_e \in (\mathbb{T}\cap [0,ta(s)] )$ , and input event $x \in X$ , the next state is given by $\delta_{ext}(q, x)=s'=(\ldots,(s_i', t_{ei}'), \ldots)$

where

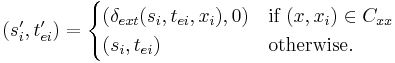
$(s_i', t_{ei}')= \begin{cases} (\delta_{ext}(s_i, t_{ei}, x_i),0) & \text{if } (x, x_i) \in C_{xx}\\ (s_i, t_{ei}) & \text{otherwise}. \end{cases}$

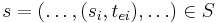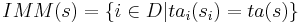Given the partial state $s=(\ldots,(s_i, t_{ei}),\ldots) \in S$ , let $IMM(s)=\{i \in D| ta_i(s_i) = ta(s) \}$ denote the set of imminent components. The firing component 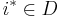$i^* \in D$ which triggers the internal state transition and an output event is determined by

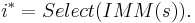
$i^* = Select(IMM(s)).$

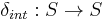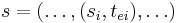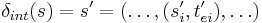
$\delta_{int}:S \rightarrow S$ is the internal state function. Given a partial state $s=(\ldots, (s_{i}, t_{ei}),\ldots)$ , the next state is given by $\delta_{int}(s)=s'=(\ldots,(s_i', t_{ei}'), \ldots)$

where

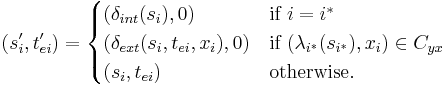
$(s_i', t_{ei}')= \begin{cases} (\delta_{int}(s_i),0) & \text{if } i = i^*\\ (\delta_{ext}(s_i, t_{ei}, x_i),0) & \text{if } (\lambda_{i^*}(s_{i^*}), x_i) \in C_{yx}\\ (s_i, t_{ei}) & \text{otherwise}. \end{cases}$

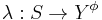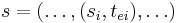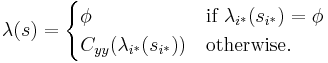
$\lambda:S \rightarrow Y^\phi$ is the output function. Given a partial state $s=(\ldots, (s_{i}, t_{ei}),\ldots)$ , $\lambda(s)= \begin{cases} \phi &\text{if } \lambda_{i^*}(s_{i^*})=\phi \\ C_{yy}(\lambda_{i^*}(s_{i^*})) &\text{otherwise}. \end{cases}$

View2: Total States = States * Lifespan * Elapsed Times

Given a coupled DEVS model 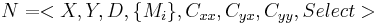$N = <X,Y,D,\{M_i\},C_{xx}, C_{yx}, C_{yy}, Select>$ , its behavior is described as an atomic DEVS model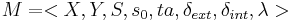 $M = <X,Y,S,s_0,ta, \delta_{ext}, \delta_{int}, \lambda>$

where

$X$ and $Y$ are the input event set and the output event set, respectively.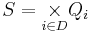
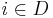$S=\underset{i \in D}\times Q_i$ is the partial state set where $Q_i=\{(s_i,t_{si}, t_{ei})| s_i \in S_i, t_{si} \in \mathbb{T}^\infty, t_{ei} \in (\mathbb{T} \cap [0, t_{si}])\}$ is the total state set of component $i \in D$ (Refer to View2 of Behavior of DEVS).
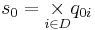$s_0=\underset{i \in D}\times q_{0i}$ is the initial state set where 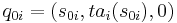$q_{0i}=(s_{0i},ta_i(s_{0i}),0)$ is the total initial state of component $i \in D$ .

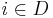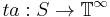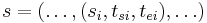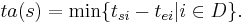
$ta:S \rightarrow \mathbb{T}^\infty$ is the time advance function. Given $s=(\ldots, (s_{i},t_{si},t_{ei}),\ldots)$ , $ta(s)= \min\{ t_{si} - t_{ei}| i \in D\}.$

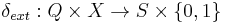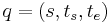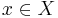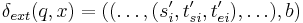
$\delta_{ext}:Q \times X \rightarrow S \times \{0, 1\}$ is the external state function. Given a total state $q=(s,t_s,t_e)$ where $s=(\ldots, (s_{i}, t_{si},t_{ei}),\ldots), t_s \in \mathbb{T}^\infty, t_e \in (\mathbb{T}\cap [0,t_s] )$ , and input event $x \in X$ , the next state is given by $\delta_{ext}(q, x)=((\ldots,(s_i', t_{si}', t_{ei}'), \ldots),b)$

where

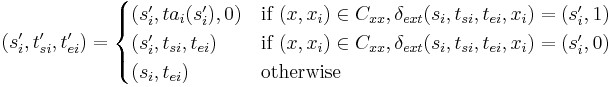
$(s_i', t_{si}', t_{ei}')= \begin{cases} (s_i', ta_i(s_i'), 0) & \text{if } (x, x_i) \in C_{xx},\delta_{ext}(s_i, t_{si}, t_{ei}, x_i)=(s_i',1)\\ (s_i', t_{si}, t_{ei} ) & \text{if } (x, x_i) \in C_{xx},\delta_{ext}(s_i, t_{si}, t_{ei}, x_i)=(s_i',0)\\ (s_i, t_{ei}) & \text{otherwise} \end{cases}$

and

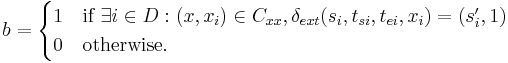
$b= \begin{cases} 1 & \text{if } \exists i \in D: (x, x_i) \in C_{xx},\delta_{ext}(s_i, t_{si}, t_{ei}, x_i)=(s_i',1)\\ 0 & \text{otherwise}. \end{cases}$

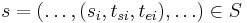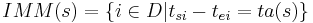Given the partial state $s=(\ldots,(s_i, t_{si}, t_{ei}),\ldots) \in S$ , let $IMM(s)=\{i \in D| t_{si} - t_{ei} = ta(s) \}$ denote the set of imminent components. The firing component 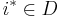$i^* \in D$ which trigers the internal state transition and an output event is determined by

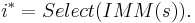
$i^* = Select(IMM(s)).$

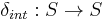$\delta_{int}:S \rightarrow S$ is the internal state function. Given a partial state 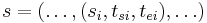$s=(\ldots, (s_{i},t_{si}, t_{ei}),\ldots)$ , the next state is given by $\delta_{int}(s)=s'=(\ldots,(s_i', t_{si}', t_{ei}'), \ldots)$

where

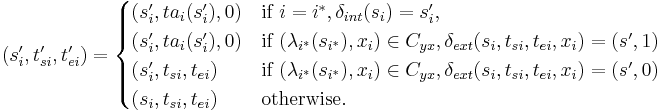
$(s_i', t_{si}', t_{ei}')= \begin{cases} (s_i', ta_i(s_i'),0) & \text{if } i = i^*,\delta_{int}(s_i)=s_i',\\ (s_i', ta_i(s_i'),0) & \text{if } (\lambda_{i^*}(s_{i^*}), x_i) \in C_{yx},\delta_{ext}(s_i, t_{si}, t_{ei}, x_i)=(s', 1)\\ (s_i', t_{si}, t_{ei}) & \text{if } (\lambda_{i^*}(s_{i^*}), x_i) \in C_{yx},\delta_{ext}(s_i, t_{si}, t_{ei}, x_i)=(s', 0)\\ (s_i, t_{si}, t_{ei}) & \text{otherwise}. \end{cases}$

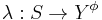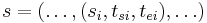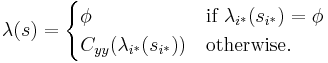
$\lambda:S \rightarrow Y^\phi$ is the output function. Given a partial state $s=(\ldots, (s_{i}, t_{si}, t_{ei}),\ldots)$ , $\lambda(s)= \begin{cases} \phi &\text{if } \lambda_{i^*}(s_{i^*})=\phi \\ C_{yy}(\lambda_{i^*}(s_{i^*})) &\text{otherwise}. \end{cases}$

Time Passage

Since in a coupled DEVS model with non-empty sub-components, i.e., 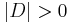$|D|>0$ , the number of clocks which trace their elapsed times are multiple, so time passage of the model is noticeable.

For View1

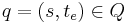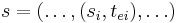
Given a total state $q=(s,t_e) \in Q$ where $s = (\ldots,(s_i, t_{ei}),\ldots)$

If unit event segment $\omega$ is the null event segment, i.e. $\omega=\epsilon_{[t, t%2Bdt]}$ , the state trajectory in terms of Timed Event System is

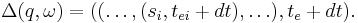
$\Delta(q, \omega)=((\ldots,(s_i, t_{ei}%2Bdt),\ldots), t_e%2Bdt).$

For View2

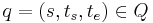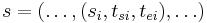
Given a total state $q=(s,t_s,t_e) \in Q$ where $s = (\ldots,(s_i, t_{si}, t_{ei}),\ldots)$

If unit event segment $\omega$ is the null event segment, i.e. $\omega=\epsilon_{[t, t%2Bdt]}$ , the state trajectory in terms of Timed Event System is

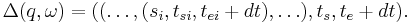
$\Delta(q, \omega)=((\ldots,(s_i,t_{si}, t_{ei}%2Bdt),\ldots), t_{s}, t_e%2Bdt).$

Remarks

The behavior of a couple DEVS network whose all sub-components are deterministic DEVS models can be non-deterministic if 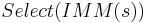$Select(IMM(s))$ is non-deterministic.

References

[Zeigler84] Bernard Zeigler (1984). Multifacetted Modeling and Discrete Event Simulation. Academic Press, London; Orlando. ISBN 978-0127784502.
[ZKP00] Bernard Zeigler, Tag Gon Kim, Herbert Praehofer (2000). Theory of Modeling and Simulation (second ed.). Academic Press, New York. ISBN 978-0127784557.

Behavior of coupled DEVS

Contents

View1: Total States = States * Elapsed Times

View2: Total States = States * Lifespan * Elapsed Times

Time Passage

Remarks

See also

References